Reti neurali ricorrenti (RNN), cosa sono, come funzionano

La rete neurale ricorrente (RNN) è una variante delle reti neurali artificiali (ANN) che vengono usate con successo con dati sequenziali. Strutturalmente organizzate come le ANN, le RNN hanno caratteristiche funzionali che le rendono particolarmente efficienti per l’analisi delle serie temporali.

Il termine “reti neurali ricorrenti” fa riferimento all’inclusione di connessioni cicliche, dove un output di un layer (o livello) è riportato come input di un layer precedente. Questa caratteristica le rende particolarmente adatte alla simulazione di dati in sequenze temporali; inoltre, possono essere molto efficaci in contesti dove la dipendenza temporale nei non è nota a priori ed è una caratteristica implicita del modello.

Le tre reti neurali

Le reti neurali possono essere distinte in tre macro classi:

• la generica rete neurale a molti layer, ad esempio il Multi Layer Perceptron perché ogni singolo layer è costruito sulla base l’algoritmo perceptron. Non possono gestire dati sequenziali; sono molto efficienti nell’utilizzo di dati in forma tabellare.
• CNN: le reti neurali convoluzionali, molto efficienti nelle applicazioni a problemi con immagini e video; in generale adatte all’ambito della computer vision. Lavorano sulla convoluzione delle immagini con dei filtri per estrarre le caratteristiche delle immagini. Sono complesse da progettare e da manutenere; possono essere lente a causa della grande quantità di parametri e di layer nascosti.
• RNN: le reti neurali ricorrenti; hanno la possibilità di condividere i parametri in diversi passi temporali diminuendone il numero e quindi diminuendo il costo computazionale rispetto alle due precedenti.

Come funzionano le reti neurali

Le reti neurali artificiali (ANN) sono definite così perché si ispirano al processo biologico di apprendimento di un cervello umano. Una ANN è un potente e versatile strumento matematico in grado di svolgere complessi compiti di classificazione, regressione, approssimazione di funzioni, serie temporali. Le loro caratteristiche di successo dipendono dalla capacità di apprendere e migliorarsi attraverso l’esperienza; inoltre, per la loro natura non lineare permettono di affrontare problemi complessi ove gli algoritmi di Machine learning hanno poco successo anche se a discapito di una perdita di spiegabilità. Le ANN sono in grado di gestire relazioni non lineari molto complesse tra i dati e questo le rende adatte anche per risolvere problemi multidimensionali.

L’architettura di una ANN consiste in molti neuroni artificiali detti nodi organizzati in molti layer connessi tra loro. I nodi di un layer sono connessi ai nodi del layer successivo.

La struttura di base minima consiste di tre layer:

• Input: è quello che riceve i dati che devono essere elaborati dalla rete
• Hidden (nascosto): insieme di uno o più layer che modellano il sistema analizzato, ricevono i dati dal layer di input, li elaborano e passano il risultato al layer di output. Sono detti nascosti perché non accessibili e racchiusi tra input e output.
• Output: fornisce il risultato finale sulla base delle trasformazioni eseguite negli hidden layer.

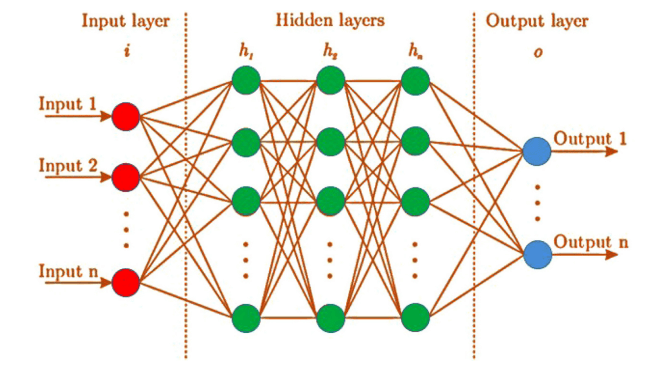
In questa immagine è rappresentata l’architettura di base di una rete neurale artificiale.

In una rete ogni nodo ha un valore detto peso; per i nodi nascosti il peso è calcolato sulla base dell’architettura della rete. I nodi di input hanno come peso i dati forniti alla rete. I nodi di output hanno come peso i risultati finali prodotti dalla rete. Il peso di un nodo in input viene elaborato e contribuisce al peso dei nodi a cui è connesso nel layer successivo. La trasformazione dei dati da un layer al successivo avviene tramite la funzione di attivazione e la minimizzazione della funzione di costo, ovvero una funzione che rappresenta l’errore fra il risultato calcolato e il valore reale dell’output.

La funzione di attivazione

Una funzione di attivazione definisce come trasferire i pesi dai nodi di un layer ai nodi del layer successivo. In questa operazione i segnali lineari possono essere trasformati in non lineari creando un enorme capacità di apprendimento di processi complessi. La funzione di attivazione svolge diverse operazioni e calcoli; la scelta della funzione di attivazione dipende dal dominio di applicazione e concorre a determinare risultati ottimali.

Le funzioni di attivazione possono essere principalmente di due tipi:

• lineari: l’output è proporzionale all’input, ad esempio, a un raddoppio del valore di input corrisponde un raddoppio del valore di output. Questo tipo di funzioni di attivazione non sono molto utili per reti in cui si usa la “back-propagation”, tipica delle reti ricorrenti.
• non lineari: l’output è una elaborazione complessa dell’input; queste funzioni son usate ampiamente nelle reti neurali perché ne caratterizzano l’efficienza e la qualità dei risultati.

La funzione di costo

La minimizzazione della funzione di costo e quindi dell’errore sull’output, realizza l’ottimizzazione dei pesi di ogni nodo per minimizzare l’errore sull’output. Un algoritmo molto usato per minimizzare la funzione di costo è la discesa del gradiente, una sorta di discesa lungo un pendio fino a trovare il punto di minimo; questo algoritmo è molto efficace quando la funzione di costo è una funzione quadratica, per esempio quando è definita come la somma dei quadrati degli errori, ma non sempre è così ed è il caso delle reti neurali. Il raggiungimento del punto di minimo viene detto convergenza e il numero di passi (epoch) con cui viene raggiunto dipende dal tasso di apprendimento, uno dei parametri del modello. Un tasso di apprendimento troppo alto, per assurdo, può portare a non raggiungere mai la convergenza, mentre un tasso troppo basso può richiedere troppi passi e quindi allungare molto la fase di addestramento. La soluzione ottimale è di ridurre il tasso di apprendimento contestualmente all’avvicinamento al punto di minimo, che corrisponde alla diminuzione di quello che è chiamato gradiente. In caso di funzioni di costo più complesse ci sono diversi punti di minimo detti locali; quindi, corrispondenti a un addestramento non ottimale; in questi casi si adottano algoritmi più efficienti (per esempio citiamo solo il gradiente stocastico) che consentono di avvicinarsi molto a un minimo globale.

In breve, il funzionamento di una rete neurale si può riassumere così: partendo dal livello di input, i dati vengono propagati in avanti (feed forward) da un livello al successivo tramite la funzione di attivazione; ogni livello fa da input al livello successivo fino al livello di output. Sulla base dell’output viene calcolato un errore tramite la funzione di costo che deve essere minimizzata. L’errore calcolato viene propagato all’indietro (back propagation) per aggiornare i pesi (quindi il modello) e ripetere il procedimento per un dato numero di epoch fino al raggiungimento del minimo ottimale.

Reti neurali ricorrenti e dati di serie temporali

In una RNN un hidden layer riceve l’input sia dal layer precedente dello stesso istante temporale, sia dal layer dell’istante temporale precedente. La rappresentazione grafica è fatta con un ciclo che parte dal nodo e torna sullo stesso nodo, questa è la ragione per cui è stata chiamata ricorrente. L’immagine seguente ne mostra una rappresentazione.

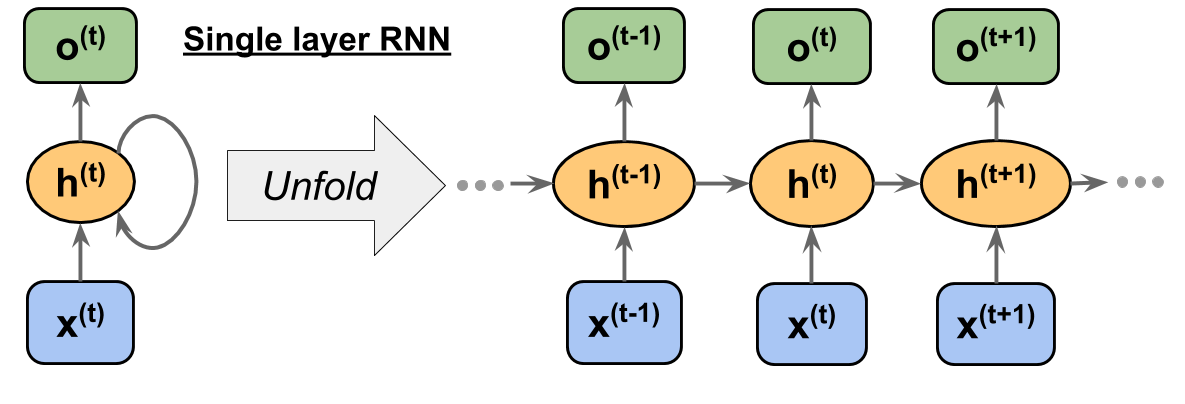
Immagine da “Python Machine Learning” – Sebastian Raschka, Vahid Mirjalili – PACKT

Negli algoritmi di Machine learning supervisionato si assume che i dati di input siano indipendenti e identicamente distribuiti, ovvero il training dataset è costituito da dati indipendenti tra loro e con la stessa distribuzione sottostante; i dati possono essere utilizzati in qualsiasi ordine. Queste assunzioni non sono valide nel caso di sequenze, perché si parla di dati sequenziali. Le serie temporali sono un particolare tipo di dati sequenziali, hanno una dimensione per il tempo che ne determina l’ordine. Diversamente un testo o un DNA sono rappresentati da sequenze ma non associate a una dimensione temporale.

Una RNN per gestire dati in sequenza deve avere una memoria e ricordare i dati già processati. Questa peculiarità dei dati in sequenza complica l’addestramento delle RNN. Le serie temporali, essendo ordinate temporalmente, hanno le caratteristiche per essere una tipologia di dati difficile da modellare con una RNN.

Lavorando su dati sequenziali, una RNN effettua le stesse operazioni su ogni elemento delle sequenze di input; l’output ad ogni passo dipende da input e calcoli precedenti nel tempo; questa modalità consente di avere una memoria degli eventi precedenti, implicitamente codificati nei layer nascosti. Teoricamente una RNN può memorizzare sequenze arbitrariamente lunghe, in realtà la memoria è limitata dalla dimensione finita della rete e soprattutto da un insieme di parametri non ottimale. Per superare i limiti nella memorizzazione delle informazioni sono state ideate diverse architetture di RNN, alcune di queste includono memorie permanenti esterne.

Diversamente da altri modelli lineari adottati per scopi predittivi, le RNN hanno la capacità di apprendere modelli di complessità arbitraria gestendo serie temporali con effetti fortemente non lineari. Tutta questa potenza non è necessaria, anzi potrebbe essere controproducente se la dipendenza temporale tra i dati è ridotta a dei piccoli intervalli di tempo; in questi casi danno migliori risultati algoritmi quali ARIMA, SVM. In tutte le situazioni in cui il sistema analizzato è caratterizzato da lunghe dipendenze temporali e non sono disponibili a priori delle informazioni, le RNN rappresentano la miglior soluzione.

Tipologie di RNN

A loro volta le RNN, in base alla loro architettura possono essere classificate in diversi modi. Una prima suddivisione è sulla base del tipo di dati in input e output:

• Many-to-one: i dati di input sono una sequenza mentre l’output non lo è. Un tipico esempio è la sentiment analysis, dove l’input è una frase, quindi una sequenza di parole, mentre l’output è un’etichetta che indica il “sentiment”.
• One-to-many: è l’opposto della precedente, in input ci sono dati non in sequenza mentre l’output è una sequenza. Un esempio è l’annotazione di immagini, in input abbiamo delle immagini e per ognuna in output abbiamo una didascalia, un testo che descrive l’immagine.
• Many-to-many: sono reti in cui sia l’input sia l’output sono sequenze. Esempi di questi modelli sono la traduzione da una lingua a un’altra; la classificazione di video, dove ogni singola immagine del video viene etichettata.

Delle notevoli applicazioni delle RNN includono la modellazione di un linguaggio e la traduzione del linguaggio naturale, il riconoscimento vocale, il riconoscimento della scrittura manuale. In molti contesti viene usata una variante particolare di RNN, detta Long-Short-Term-Memory (LSTM) perché ha la capacità di memorizzare informazioni per periodi di tempo molto lunghi.

Una ulteriore suddivisione delle RNN si basa sulla loro architettura:

• RNN standard, composta da livelli nascosti di tipo ricorrente; può gestire modelli dove l’input è una sequenza, l’output può essere una sequenza (many-to-many) o l’ultimo output della sequenza (many-to-one).
• LSTM (Long Short Term Memory): in questa architettura I livelli nascosti di una generica RNN sono sostituiti da celle di memoria. Il flusso delle informazioni all’interno di una cella è regolato da unità di calcolo dette “gates”. In ogni cella di memoria ci sono tre tipi di gate, uno effettua il reset dello stato della cella, uno è responsabile dell’aggiornamento dello stato, l’ultimo decide come deve essere eseguito l’aggiornamento delle unità nascoste. Sebbene sembri molto complessa come architettura, sia in Pytorch sia in Tensorflow sono già implementati i metodi per creare i modelli corrispondenti.
• GRU (Gated Recurrent Unit): hanno un’architettura più semplice delle LSTM e sono più efficienti dal punto di vista computazionale ma con risultati paragonabili. Simili alle LSTM, non hanno celle di memoria separate, per cui la complessità architetturale è inferiore.

Addestramento delle reti neurali ricorrenti

L’addestramento di una RNN ricalca quello di una ANN generica; i livelli aggiunti nel modello determinano l’architettura e la tipologia della rete. I framework disponibili sul mercato, come per esempio Tensorflow e Pytorch, offrono layer ricorrenti con i parametri per configurare l’utilizzo di sequenze. Un layer ricorrente può restituire una sequenza in output oppure l’ultimo tra gli output della sequenza.

Un algoritmo di apprendimento delle RNN è il BPTT (Back Propagation Through Time) e risale al 1990 per opera di Paul Werbos ( Backpropagation through time: what it does and how to do it | IEEE Journals & Magazine | IEEE Xplore). La derivazione dei gradienti è più complessa rispetto ad una rete neurale classica, ma l’idea di base è che la funzione di costo globale sia la somma di tutte le funzioni di costo in tutti gli intervalli di tempo, dal temo t₁ al tempo t_n finale. Poiché al generico tempo t la funzione di costo dipende da tutti i passi precedenti, il calcolo si complica sempre di più all’aumentare del tempo e contribuisce a un problema noto come “vanishing” e “exploding” dei gradienti; in altre parole questo problema si può pensare come la riduzione o la crescita eccessiva dei pesi di ogni livello nascosto ricorrente.

Questo problema è stato affrontato in diverse pubblicazioni scientifiche, per esempio in On the difficulty of training Recurrent Neural Networks (arxiv.org). Le soluzioni a questo problema sono varie; le più immediate sono di mettere una soglia al valore del gradiente e di limitare il numero di passi di tempo per cui l’algoritmo può aggiornare all’indietro i pesi. Una soluzione più elaborata è un’architettura di tipo LSTM.

Limitazioni delle RNN

Una limitazione caratteristica delle reti neurali che si cerca di aggirare è che si presenta come una black-box e nasconde la “spiegabilità” del modello; si ottengono ottimi risultati ma si perde la padronanza nel capire cosa determina un output specifico rispetto a un altro.

Altri limiti di tutte le reti neurali sono sicuramente l’elevata dimensionalità delle caratteristiche, il numero molto elevato dei coefficienti di peso e la forma della funzione di costo che presenta molti minimi locali ma non ottimali in quanto deviano dal minimo globale che è quello che si cerca di raggiungere. In questo scenario, ha un ruolo importante il controllo del gradiente, tipico di ogni architettura che lo utilizzi per minimizzare la funzione di costo. Il controllo dei gradienti richiede molte risorse computazionali e rallenta l’apprendimento della rete tanto che spesso viene attivato solo a scopo di debug o su pochi campioni del dataset di addestramento.

Le RNN presentano una ulteriore complicazione dovuta alla presenza di una componente temporale; questo le rende difficili da addestrare perché nel meccanismo di back-propagation si possono amplificare i problemi citati di “vanishing” e “explosion”, nel calcolo del gradiente.

Sempre a causa della presenza della componente temporale, non è possibile parallelizzare le fasi di addestramento, rendendo lenta e onerosa tale operazione.

All’aumentare della lunghezza delle sequenze sia l’addestramento sia l’utilizzo della rete diventano onerosi, ragione per cui la lunghezza delle sequenze è un limite delle RNN.

Dal 2017, una nuova alternativa è stata proposta e ampiamente usata con successo, i “transformer”.