Il Test di Turing è noto ed è stato affrontato dal momento della sua formulazione in tutte le modalità. È anche stato confutato. E potremmo affrontarlo in più modi ma in questa trattazione proveremo a raccontarlo ai non addetti ai lavori. Trattiamolo subito qui in poche parole, e proviamo poi a raccontarne le implicazioni non solo per l’intelligenza artificiale, ma anche per la filosofia, e l’etica.
Cos’è il Test di Turing: “il gioco dell’imitazione”
Il Test di Turing nasce come un criterio per determinare se una macchina sia in grado di pensare come un essere umano. Tale criterio è stato suggerito da Alan Turing nell’articolo “Computing machinery and inte lligence”, apparso nel 1950 sulla rivista Mind. Nell’articolo Turing prende spunto da un gioco, chiamato “gioco dell’imitazione”, a tre partecipanti: Bob, Alice, e una terza persona, Charlie, che è tenuta separata dagli altri due e può solo stabilire tramite una serie di domande qual è l’uomo e qual è la donna. Dal canto loro anche Bob e Alice hanno dei compiti: Bob dovrebbe ingannare Charlie e portarlo a fare un’identificazione errata, mentre Alice dovrebbe aiutarlo a mantenere una identificazione corretta. Poiché bisogna privare Charlie di indizi per “indovinare” (come l’analisi della grafia o della voce), le risposte alle domande di Charlie devono essere dattiloscritte o trasmesse comunque in modo impersonale o anonimo.
È semplice come una chat telefonica di gruppo tra amici, in cui dovete capire se la cugina della vostra amica si è sostituita a lei sottraendole il telefono e sta flirtando con voi illudendovi di essere disposta a una storia: riusciremmo a scoprire l’inganno? Pensiamoci: saremmo troppo impegnati a mantenere viva la conversazione per fare improvvisamente domande sconvenienti sull’autenticità dell’interlocutore. Dovremmo essere continuamente disposti a interrompere la “magia” del flirt con una domanda improvvisa “di controllo” sul genere: “Scusa se te lo chiedo, ma ricordi cosa ti ho risposto l’altro ieri quando mi hai domandato se volevo acquistare un nuovo computer?”. Dalla risposta dovremmo riuscire a dedurre se chi sta dall’altra parte di Whatsapp sta effettivamente “imitando” il comportamento della cugina, o è autenticamente lei. Ovviamente – esattamente come nel test di Turing – a nulla varrebbero affermazioni eclatanti come “sono davvero io, Alice!” perché chiunque potrebbe affermare con forza una menzogna, senza doverla dimostrare.
Anche il test di Turing si basa sul presupposto che qualcuno o qualcosa (una macchina o un algoritmo) si sostituisca improvvisamente e a all’insaputa di tutti a Bob. Se la percentuale di volte in cui Charlie indovina chi sia l’uomo e chi la donna è simile prima e dopo la sostituzione di Bob con la macchina, allora l’algoritmo dovrebbe essere considerato intelligente, dal momento che – in questa situazione – sarebbe indistinguibile da un essere umano.
Programmi a confutazione del test: Eliza. Le varianti: la “stanza cinese”
Il test di Turing è stato via via riformulato durante gli anni. Le ragioni sono varie e passano dall’imprecisione della formulazione originale, al sorgere di nuovi problemi relativi alla definizione di macchina intelligente. A volte semplici programmi, come ad esempio Eliza (un programma che emula un terapista rogersiano), hanno costretto a riformulare i criteri del test perché inadeguati o troppo facilmente soddisfatti da programmi evidentemente non pensanti.

Il filosofo John Searle ha proposto una modifica al test di Turing, che ha preso il nome di “stanza cinese”, sostenendo l’inattendibilità del test di Turing come prova sufficiente a dimostrare che una macchina o un qualsiasi sistema informatico siano sistemi dotati di vera intelligenza, sia che questi abbiano superato o no tale test. Numerose altre versioni del test di Turing, comprese quelle esposte sopra, sono state sollevate nel corso degli anni.
Come funziona il Test di Turing
“Se fai le cose per bene, nessuno sospetterà che tu abbia fatto davvero qualcosa. [Dio]”
(Futurama – episodio “Bender e Dio”, Matt Groening e David X. Cohen)
In una puntata del cartoon “Futurama” di Matt Groening e David X. Cohen, dal titolo “Bender e Dio”, viene prospettata la possibilità che “se fai le cose per bene, nessuno sospetterà che tu abbia fatto davvero qualcosa” da parte di un Dio pangalattico che dialoga direttamente con il robot Bender, il beniamino dotato di AI della serie Futurama.
In questo cartone animato, viene attribuito a Dio il “gioco dell’Imitazione” – the Imitation game – come viene chiamato nel titolo dell’omonimo film su Alan Turing, da cui il famoso test prende il nome. Mentre questo test viene generalmente ascritto alle tematiche connesse con l’intelligenza artificiale, il tema riguarda invece la capacità di nascondere una operazione intenzionale dietro un fatto che all’apparenza deve risultare casuale, proprio come farebbe un Dio che, operando come demiurgo, volesse rimanere celato o comunque lontano dalle umane miserie alla maniera degli dei greci. Sostanzialmente un gioco imitativo (“the imitation game”): interpretare cioè un ruolo in modo talmente naturale, da lasciar intendere a un osservatore che gli eventi abbiano avuto il loro corso in modo del tutto spontaneo e senza intervento terzo alcuno.
È questo ciò che campeggia alla base del test di Turing: non una sfida a una intelligenza artificiale di comportarsi in modo umano, ma una sfida a un algoritmo a nascondersi mimetizzandosi nella casualità fino a dare l’impressione di non esistere.
Test di Turing: domande, risposte ed errori

Nel racconto “The Imitation Game” scritto da Andrew Hodges su Alan Turing (titolo originale: “Storia di un Enigma”) viene mostrato nel suo adattamento cinematografico che, durante una serata in un bar, a Turing viene un lampo di genio: la crittografia usata dalla macchina Enigma usata durante la II guerra mondiale per criptare gli ordini impartiti agli U-Bot da parte del comando tedesco, non è casuale.
Turing si costringe a pensare allora che bisogna restringere il campo infinito di parole casuali di cui cercare il significato a partire dalle più ripetitive, ad esempio quelle che compaiono nei bollettini meteorologici dei nazisti (ne viene inviato uno ogni mattina alle 6, come primo messaggio del giorno, e tutti iniziano e finiscono sempre con le stesse parole). Nel film (e nel racconto) il gruppo di Turing riesce, grazie a questa intuizione, a decifrare un messaggio che parla di un imminente attacco al convoglio alimentare Carlisle.
Da quel momento in poi, in cui la casualità della chiave di criptazione viene messa in seria confutazione, sarà questione di momenti arrivare a identificare la chiave principale per decrittare i messaggi.
Nel caso specifico, viene affrontato il paradosso che si riesca a simulare la casualità perfetta non attraverso la vera casualità, (lancio di dadi, monetina, estrazione casuale da sequenze infinite) ma adottando un procedimento che la generi in modo algoritmico, senza perdere però l’imprevedibilità.
Dopo aver spiegato la natura del suo test, Turing prosegue facendo alcune osservazione che, per l’anno in cui scrive, sono molto avanzate. Per cominciare, presenta un breve dialogo ipotetico tra interrogante e interrogato.
- Domanda: Per cortesia, mi scriva un sonetto che tratti del ponte sul Forth [un ponte sul fiordo di Forth, in Scozia].
- Risposta: Non faccia affidamento su di me per questo, non ho mai saputo scrivere poesie.
- Domanda: Sommi 34957 a 70764
- Risposta: (Pausa di circa 30 secondi e poi la risposta) 105621.
- Domanda: Gioca a scacchi?
- Risposta: Sì.
- Domanda: Ho il Re in E1 e nessun altro pezzo. Lei ha solo il Re in E3 e una Torre in H8. Tocca lei a muovere. Che mossa fa?
- Risposta: (Dopo una pausa di 15 secondi) Torre in H1, matto.
Pochi lettori notano che nel problema aritmetico non solo vi è un ritardo eccessivamente lungo, ma che inoltre la risposta è sbagliata! La cosa sarebbe giustificata se colui che risponde fosse un essere umano: un semplice errore di calcolo. Ma se a rispondere fosse una macchina, sono possibili varie spiegazioni. Eccone alcune:
- un errore casuale a livello hardware (cioè un evento non-riproducibile)
- un errore non voluto a livello hardware o di programmazione che (in modo ripetibile) causa errori aritmetici;
- un atto inserito volutamente dal programmatore (o dal costruttore) della macchina per introdurre occasionali errori aritmetici, in modo da ingannare gli interroganti;
- un epifenomeno non previsto: il programma fa fatica a pensare in termini astratti e, semplicemente, ha commesso un “errore genuino”, che potrebbe non ripetere la prossima volta
- uno scherzo da parte della macchina stessa, che ha fatto volontariamente un dispetto all’interrogante.
Se si riflette su ciò che Turing potrebbe aver voluto dire con questo delicato tocco, vi si trovano accennati proprio quasi tutti i principali temi filosofici connessi con la moderna intelligenza artificiale.
Perché un algoritmo non può generare un risultato a caso
La (brutta?) notizia, è che non è possibile dissimulare comportamenti casuali mediante un computer tradizionale e che occorrono molti artifici anche solo per fare in modo che una macchina riesca a simulare una sequenza di numeri casuali. I numeri casuali sono fondamentali per i criteri di crittografia che proteggono le nostre mail, password, pin della carta di credito. Ma come dicevamo prima i numeri casuali sono importanti perché sono alla base dei videogame. I numeri casuali sono alla base di praticamente tutti, i videogiochi, e questa è una ragione più che sufficiente per studiarne delle caratteristiche che possono rivelarsi interessanti. Come abbiamo spiegato intuitivamente precedentemente, un numero casuale viene generato, in un qualsiasi computer moderno, usando un qualsiasi linguaggio di programmazione (c/c++, pPython, MatLab per citare quelli maggiormente usati per il calcolo scientifico) addivenendo ad una sequenza di numeri casuali generata mediante un algoritmo scritto in qual particolare linguaggio.
E da qui il paradosso: poiché un algoritmo è una insieme di istruzioni o di passi o di azioni da compiere per manipolare un dato in input in modo da ottenere un dato di output e questa sequenza di passi deve essere ben determinata, ne consegue che un algoritmo non può generare un risultato “a caso”. Inoltre la prerogativa più importante di un algoritmo è che, dato lo stesso input viene generato sempre lo stesso output. Quindi – allo stesso modo – se continuo a fornire all’algoritmo dell’addizione gli addendi “2” e “2”, allora continuerò ad ottenere la somma “4” così come per generare una sequenza di numeri casuali. Anche per la sequenza di numeri casuali utilizzerò un processo per generarli, e poiché questo processo algoritmico non è anch’esso casuale (stesso input genera lo stesso output) si evince da se che non è possibile generare numeri casuali mediante un normale computer o linguaggio di programmazione.
Oggi sono disponibili diversi algoritmi per la generazione di numeri “non casuali” ma che si comportano come tali, i così detti numeri pseudo-casuali. Gli algoritmi oggi utilizzati sono di differente complessità e richiedono diversi tempi di esecuzione. Quanto maggiore è la complessità tanto maggiore sarà la casualità dei numeri generati. In realtà, quello che cambia tra i vari metodi, è il numero di valori da dover tirare fuori prima che una ripetizione o schema possa essere trovato all’interno della sequenza (ricordate l’assenza delle cifre 5 e 6 dalla mia tastiera?). Gli algoritmi oggi utilizzati maggiormente non generano davvero numeri casuali, e comunque se lo fanno, non ne generano all’infinito. Generano cioè una sequenza pseudo-casuale con un numero finito di termini, grande, certo, ma non infinito. Cosa vuol dire? Vuol dire che se ci mettiamo a scrutare con attenzione la sequenza che viene generata, la nostra pazienza presto o tardi verrà ricompensata perché dopo un certo punto la sequenza comincerà a ripetersi uguale a se stessa.
Proviamo a generare numeri casuali imprevedibili digitando numeri a caso sulla tastiera di un computer: ad esempio “0,2,9,4,8,2,3,7,1,0,9,3,8,4,7,….” etc etc. Anche se questi numeri sono stati generati casualmente, potrei a lungo andare cercare di intuire se sono stati generati da un essere umano o da un computer, magari notando che mancano le cifre “5” e “6”, potrei desumere che questi numeri sono stati digitati con 4 dita della mano sinistra e 4 dita della mano destra sulla riga dei numeri della tastiera “Qwerty”. Quindi potrei prevedere che digitassi di nuovo casualmente dei numeri sulla stessa struttura: “9,8,7,4,1,0,9,2,7,4,1,2,9,4,7,8,”, tornerebbero a mancare di nuovo le due cifre “5” e “6”, e poter fare previsioni affidabili su numeri casuali, vuol dire sostanzialmente averne annullato la casualità almeno entro certi limiti di prevedibilità.
Siamo in grado solo di essere pseudo-casuali
- LCG (linear congruential generator o generatori lineari congruenziali); furono i primi a essere sviluppati e sono tutt’ora i più utilizzati in quanto presentano un buon compromesso tra velocità e livello di complessità.
- Lagged Fibonacci, o generatori di Fibonacci ritardati; più complessi dei precedenti con un periodo di prima di ripetersi (algoritmo Twister).
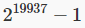
I due algoritmi esposti sono dei generatori di numeri casuali che usano, rullo di tamburi, un’equazione per generare la sequenza di numeri casuali.
LCG
Nel caso di generatori LCG la funzione implementata è
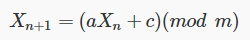
dove a, c e m sono numeri scelti per generare la sequenza. L’operazione (mod m) indica il resto della divisione tra il primo termine tra parentesi tonde ed m. Per questa sequenza il periodo massimo prima di una ripetizione è pari al valore di m; in pratica questa condizione si verifica solo per particolari scelte dei parametri a, c ed m e risulta quindi essere sempre minore. Questo algoritmo, tre le tante applicazioni, è utilizzato dalle API random di java, da gcc e da Borland per la propria distribuzione di C/C++ e Pascal.
Lagged Fibonacci
Il secondo algoritmo, il lagged Fibonacci, ha invece un’equazione simile a quella utilizzata per generare una sequenza di Fibonacci, da cui prende il nome:
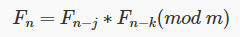
in questo caso * indica una qualsiasi operazione binaria. Nel caso l’operatore sia la moltiplicazione l’algoritmo viene detto moltiplicativo o ritardato. Anche in questo caso l’algoritmo ha un periodo che dipende dalle particolari scelte di k ed m. In particolare per questo tipo di algoritmo l’uso della somma come operazione binaria aumenta il periodo rispetto all’uso della moltiplicazione.
Come opera un algoritmo generatore di numeri pseudo-casuali
Gli algoritmi ora presentati, per come sono definiti, non possono essere usati per la crittografia in quanto intrinsecamente deboli. Per scopi in cui la sicurezza è un fattore determinante occorre usare algoritmi di tipo diverso, “più sicuri” e “più casuali” – se così possiamo dire. Tra gli algoritmi usati per la crittografia uno dei più comuni è chiamato Fortuna. Tale algoritmo è in realtà una famiglia di generatori di numeri pseudo-casuali P.R.N.G. (Pseudo Random Number Generator) in quanto alcuni dei suoi parametri sono modificabili dando origine a diverse configurazioni. Il nome dell’algoritmo, Fortuna, è un chiaro richiamo alla dea del caso della mitologia greca, almeno secondo i suoi creatori Bruce Schneier e Niels Ferguson.
Come funziona l’algoritmo? Esso è composto da tre parti.
- un generatore di numeri che inizializzato con un seme genererà una sequenza di numeri casuali;
- un accumulatore di entropia che raccoglie dati da vari dispositivi (mouse, tastiera, etc) e li accumula, questi dati vengono poi utilizzati per rinnovare il seed del generatore;
- un file di seed che salva alcuni dei dati random utilizzati dal generatore in modo da inizializzarlo all’avvio del pc quando l’accumulatore di entropia non è ancora pieno.
L’algoritmo così ottenuto è quindi molto più sicuro in quanto basato su una quantità di dati generalmente molto grande e che può considerarsi più o meno casuale (pensiamo ai movimenti del mouse sullo schermo che vengono utilizzati per generare le sequenze).
Test di Turing e algoritmi casuali
Abbiamo visto che anche soltanto l’Imitation Game della casualità è praticamente impossibile, gli algoritmi casuali non esistono e quelli che chiamiamo tali in realtà non lo sono. Vengono generati tramite un algoritmo che come tale non è casuale per sua stessa definizione. Di conseguenza, le macchine e i loro algoritmi generano sequenze di numeri pseudocasuali, sequenze di numeri definite prevedibili che hanno le proprietà dei numeri casuali se presi non troppi alla volta (al massimo un numero pari al periodo) e vengono utilizzati per le applicazioni quotidiane tra cui anche i videogiochi. Esistono alcuni algoritmi che cercano di rendere le cose più complicate, acquisiscono dati random dalle periferiche (mouse, tastiera, etc) e li usano per generare delle sequenze più casuali e possono quindi essere usati per la crittografia e la sicurezza informatica.
Ma a cosa serve dissimulare la casualità imitando un comportamento grazie a un algoritmo? Al termine del lavoro di Turing sulla macchina Enigma per decifrare i codici delle trasmissioni tedesche durante la seconda guerra mondiale, si pose un dilemma. Se si fosse intervenuti in modo massiccio, decrittando automaticamente ciascun messaggio grazie al sistema messo in piedi dal gruppo di Alan Turing, si sarebbe mostrata sostanzialmente una procedura algoritmica perfetta, grazie alla quale i messaggi nemici non sarebbero più stati un mistero, e questo avrebbe fatto in modo che i tedeschi, comprendendo che è era stato trovato il modo di decifrare i loro messaggi, avrebbero di nuovo cambiato la chiave di criptaggio, stavolta in maniera ancora più profonda e inesplicabile.
Si passa allora di nuovo a un “Imitation Game” della casualità, cercando di “dosare”, “ottimizzare”, o addirittura “sbagliare” gli interventi, per minimizzare i danni e fare in modo che i tedeschi non comprendano che è stato trovato il modo di decifrare i loro messaggi.
Un piano siffatto, denso di sbagli e manchevolezze nello sventare affondamenti e missioni navali di affondamento da parte degli U-Bot, avrebbe comunque avuto elevati costi umani, ma avrebbe “simulato” una casualità di intervento che non avrebbe – se ben organizzata – instillato alcun dubbio sul fatto che i fallimenti di alcune missioni tedesche fossero dovuti alla rintracciabilità delle trasmissioni.
Il dilemma morale posto all’équipe di matematici, sebbene quasi insostenibile, ha infine successo. Finita la guerra, si festeggia con gran giubilo dei protagonisti e dell’intera nazione, e dopo diversi anni dalla missione Enigma e dalla conclusione del conflitto mondiale, si calcola che, se i messaggi di Enigma non fossero stati decifrati, la guerra sarebbe potuta durare per altri due anni provocando 14 milioni di ulteriori vittime.
Ricordiamo per dovizia di particolari che le informazioni relative al lavoro svolto da Turing con i colleghi furono tenute segrete per i 50 anni successivi.
Come una macchina ha superato il test di Turing: la storia di Eugene Gootsman
È mai riuscito, a una macchina, di superare il test di Turing? La risposta è discorde. Il caso più emblematico è quello di Eugene Goostman, un chatterbot progettato da un gruppo di programmatori russi (Vladimir Veselov, Eugene Demchenko e Sergey Ulasen) nel 2001, programmato in modo da agire e rispondere come un adolescente dell’Ucraina.
Sin dalla sua creazione, Goostman ha partecipato a numerosi test di Turing, stupendo i giudici. Si è classificato secondo al Premio Loebner, primo al Milton Keynes, il più grande evento mai realizzato per la conduzione di un test di Turing, convincendo il 29% dei giudici di essere un umano. Ancora, nel 2014, la percentuale di giudici che Gootsman è riuscito a ingannare è salita al 33%. Turing aveva predetto che entro il 2000 i computer sarebbero stati in grado di convincere il 30% di esseri umani, se sottoposti alla prova, dopo cinque minuti di conversazione. Non tutti sono concordi, però, sulla validità di questi risultati. Infatti, il test viene considerato superato se l’esaminatore sbaglia con la stessa frequenza sia quando deve distinguere un computer da un essere umano, sia quando deve distinguere un uomo da una donna.
Da Turing a Asimov, le tre leggi della robotica
La geniale intuizione di Turing è stata alla base del pensiero di un altro grande visionario dell’intelligenza artificiale, lo scrittore Isaac Asimov. Impensierito dall’avanzare dei robot, Asimov inventò le tre leggi della robotica, anticipazione della roboetica, ovvero dell’etica della robotica. Si tratta di regole che governano i rapporti tra esseri umani e robot, o meglio le diverse forme di intelligenza artificiale con le quali già conviviamo.
Le tre leggi della robotica di Asimov:
1° – Un robot non può recar danno a un essere umano né può permettere che, a causa del suo mancato intervento, un essere umano riceva danno.
2°- Un robot deve obbedire agli ordini impartiti dagli esseri umani, purché tali ordini non vadano in contrasto alla Prima legge.
3° – Un robot deve proteggere la propria esistenza, purché la salvaguardia di essa non contrasti con la Prima o con la Seconda legge.





