Le catene di Markov descrivono un processo stocastico particolare, che si presta per la creazione di modelli di sistemi che hanno un comportamento casuale nella loro evoluzione; descrivono bene fenomeni casuali che evolvono in funzione del tempo e che non hanno memoria degli stati precedenti.

Ideate e studiate dal matematico russo Andrej Markov, sono molto utilizzate per simulare sistemi in diversi campi, dalla fisica alla biologia, alla medicina, alla finanza.
Ma un altro lato interessante è che le catene di Markov sono alla base di alcuni aspetti e settori dell’intelligenza artificiale che probabilmente non si immagina: per esempio, del Part Of Speech Tagging (POS) in ambito Natural Language Processing e dell’Automatic Speech Recognition (ASR).
Vediamone l’aspetto più divulgativo e applicativo, lasciando la trattazione matematica ai lettori interessati all’approfondimento.
Cosa sono le catene di Markov
Si definisce processo stocastico una sequenza di variabili casuali {X0,X1, …. Xn,…} dove ogni Xt assume valori in un insieme finito; tipicamente ogni variabile definisce lo stato del sistema a un istante di tempo t. Un processo stocastico di questo tipo ha la proprietà di Markov oppure si dice che è un processo di Markov se la distribuzione di probabilità condizionata dello stato Xt all’istante attuale t, dipende solamente dallo stato immediatamente precedente Xt-1 e non da altri stati precedenti. In altre parole, l’evoluzione di un processo al tempo “t” dipende solo dal suo stato al tempo “t”, ovvero il processo non ha memoria!
Una catena di Markov a tempo discreto descrive un processo di Markov {Xt} in cui il parametro “t” assume solo valori discreti; tipicamente tale parametro rappresenta il tempo e assume valori interi che definiscono gli intervalli di tempo in cui l’evoluzione del processo attraversa i diversi stati. Se il parametro “t” assume valori continui si parla di catena di Markov a tempo continuo.
Una catena di Markov discreta con un numero di stati finiti può essere facilmente rappresentata:
- come matrice
- come grafo
Matrice delle probabilità di transizione
L’uso della notazione matriciale è particolarmente conveniente per valutare la distribuzione di probabilità degli stati a un passo “n” qualsiasi della catena. Si definisce la matrice P = [pij] come la matrice i cui elementi sono le probabilità che il sistema faccia una transizione dallo stato “i” allo stato “j”. La matrice è quadrata e la somma dei valori di ogni riga è 1 perché è la somma delle probabilità di transizione del sistema ad uno degli stati possibili. Gli elementi sulla diagonale rappresentano la probabilità che il sistema rimanga nello stato in cui si trova. Un esempio di matrice di transizione è la seguente in cui il sistema può trovarsi in 4 stati diversi identificati in questo caso da un numero 0,1,2,3, nella colonna a sinistra lo stato iniziale, nella riga sopra lo stato finale:
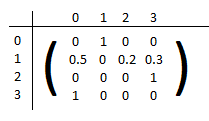
In letteratura si trovano esempi introduttivi di questo tipo e in particolare un esempio in cui gli stati sono il meteo del giorno, per esempio, soleggiato, nuvoloso, piovoso, ventilato e la matrice di transizione definisce le probabilità di evoluzione dello stato meteorologico da un giorno al successivo.
Grafo
Un modo comodo per rappresentare la matrice di transizione è un grafo dove i nodi rappresentano gli stati del sistema e gli archi rappresentano le transizioni tra gli stati. Nell’esempio seguente è rappresentato il grafo corrispondente alla matrice di transizione scritta sopra. Il grafo è orientato e in corrispondenza degli archi è riportata la relativa probabilità di transizione. Nel caso di grafi come in questo esempio è molto facile ed immediato seguire l’evoluzione del sistema. Ogni passaggio da uno stato all’altro rappresenta un passo della catena e una applicazione della matrice di transizione.
Comunque, da entrambe le rappresentazioni è possibile dedurre l’evoluzione del sistema descritto, se raggiungerà uno stato finale, se continuerà a transitare su tutti gli stati in modo periodico oppure no, se sarà di tipo oscillante fra due o più stati.
Come le catene di Markov descrivono l’evoluzione di un sistema
I modelli basati sulle catene di Markov descrivono sistemi che evolvono nel tempo per cui è possibile usarli per rispondere a domande del tipo:
- in che stato si troverà il sistema dopo N passi o intervalli di tempo
- se il sistema passa da uno stato A ad uno stato B in N passi, con che probabilità seguirà un percorso determinato?
Non tutti i sistemi possono essere descritti mediante una catena di Markov, devono essere soddisfatte alcune condizioni, tra cui la proprietà di Markov, ovvero il sistema non ha memoria, l’evoluzione da uno stato al successivo dipende solo dallo stato presente e non da quello che è successo prima; un’altra condizione è che le proprietà di transizione degli stati siano costanti nel tempo e che gli stati stessi non cambino nel tempo.
Se la matrice di transizione descrive un passo del sistema in evoluzione, per la proprietà di Markov, per descrivere N passi è sufficiente moltiplicare N volte la matrice per se stessa; per passare da uno stato iniziale a uno finale dopo N passi la matrice di di transizione sarà data da PxPxP…..xP N volte, ovvero PN. All’aumentare del numero di passi N può capitare che le probabilità di transizione, ovvero la matrice PN rimanga invariata; significa che il sistema in un determinato tempo raggiunge uno stato stazionario indipendentemente dallo stato iniziale. Se non viene raggiunto mai lo stato stazionario il sistema potrebbe attraversare tutti gli stati e avere qualche periodicità. Questi comportamenti ovviamente dipendono a caratteristiche particolari della catena di Markov e del grafo che la rappresenta. Per un approfondimento si veda [1].
Catene di Markov: alcune applicazioni
La creazione di modelli stocastici basati sulle catene di Markov è di importanza fondamentale in fisica, biologia, ingegneria, economia, finanza e scienze sociali e in generale ovunque ci siano sistemi descritti da modelli stocastici che evolvono nel tempo.
Le catene di Markov sono solo l’inizio e la base di molti modelli ad ampio spettro applicativo come i processi decisionali di Markov, i modelli a stati nascosti (Hidden Markov Models), metodi Monte Carlo (Monte Carlo Markov Chain – MCMC).
Studio di serie temporali
Una delle prime applicazioni che si può facilmente intuire è lo studio di serie temporali, ovvero sequenze di dati ordinati nel tempo che descrivono la dinamica di un sistema; in questo caso in determinate condizioni è possibile stimare la più probabile sequenza degli stati, lo stato più probabile di un sistema dopo un determinato tempo. Un esempio specifico è dato dall’analisi dell’andamento dei mercati, la previsione dei trend di mercato, la previsione del rischio finanziario.
Un tipo simile di applicazione sia ha nel caso di previsione di eventi naturali, catastrofi, terremoti; l’analisi delle serie temporali di eventi verificatisi nel passato permette tramite una catena di Markov la stima della probabilità di eventi analoghi in tempi futuri.
In modo simile si può studiare una popolazione e stimarne il tipo di evoluzione considerando le possibili transizioni degli individui dalla nascita a diversi stati di salute e sopravvivenza.
Comportamento dei clienti
Entrando più nello specifico si trovano applicazioni delle catene di Markov nello studio del comportamento dei clienti in un mercato che può essere descritto in modo probabilistico; lo scopo del modello in questo caso è l’allocazione ottimale di un budget promozionale per massimizzare la permanenza del cliente.
Studio del moto browniano
In fisica sono utilizzate per lo studio del moto browniano, ovvero del moto di piccole particelle in sospensione in fluido e più ampiamente per lo studio della dinamica dei sistemi caotici.
Nella rete internet sono di grande aiuto per la simulazione della navigazione del grafo del web e per la stima della probabilità di arrivo su determinate pagine o di abbandono di altre pagine; in altre parole, possono essere utili per il calcolo del page rank delle pagine.
Gestione delle code nei server web
In generale rovistando nella letteratura sull’argomento e tra le pubblicazioni scientifiche si trovano molti lavori e molte ricerche sui modelli di Markov e non c’è da stupirsi di quanto siano efficaci. Per esempio, si trovano applicazioni allo studio della gestione delle code nei server web, o per la rilevazione di anomalie in un sistema non necessariamente informatico, fino a casi di simulazioni per studi in campo medicale.
Conclusioni
L’argomento catene di Markov, sebbene non di popolare discussione, ci accompagna trasparentemente tutti i giorni in diversi contesti applicativi ed è oggetto di studi e ampie ricerche con applicazioni in diversi settori. Il loro utilizzo per la creazione di modelli di sistemi stocastici non è facile perché oltre alla verifica delle condizioni per l’applicabilità a un sistema, richiede la conoscenza della matematica e del formalismo matematico con cui sono state sviluppate. La loro efficacia è sicuramente competitiva rispetto ad algoritmi di Machine Learning e a volte ne sono alla base. Le catene di Markov sono anche una componente essenziale di altri metodi per modellare e studiare i sistemi dinamici come i modelli di Markov a stati nascosti (HMM), i metodi Monte Carlo con catene di Markov (MCMC), i processi decisionali di Markov.
Riferimenti
[1] Nicolas Privault – Understanding Markov Chains, examples and applications. Ed. Springer
[2] Langrock, MacDonald, Zucchini – Hidden Markov models for time series. Ed. CRC Press
[3] Ching, Huang, Kuen Siu – Markov Chains, Models, Algorithms and Applications. Ed. Springer





