Gli Hidden Markov Models (HMM) hanno il loro fondamento nelle catene di Markov e sulla proprietà di Markov che, in breve, è la mancanza di memoria degli stati passati di un sistema che evolve nel tempo. Sono molto interessanti per la creazione di modelli stocastici che descrivono l’evoluzione di eventi osservabili dipendenti da stati interni non noti. Come nel caso delle catene di Markov, un HMM descrive un processo stocastico che evolve nel tempo in modo casuale, ma il livello di complessità è tale da permettere di affrontare scenari di sistemi in cui per alcune variabili non è possibile conoscere lo stato a priori.
Cosa sono gli HMM
Una catena di Markov è composta da stati e ognuno di questi corrisponde a un evento osservabile; l’evoluzione di un sistema è una sequenza degli stati osservati negli istanti temporali. Questo modello si può estendere al caso in cui l’osservazione di uno stato non è deterministica ma dipende da un altro processo stocastico non osservabile.
In molti sistemi ci sono stati interni che non sono osservabili o determinabili per cui l’applicazione di algoritmi di Machine learning (ML) può diventare ardua; una possibile alternativa è dedurre questi stati ignoti dall’osservazione di fattori esterni. Un esempio semplice e divulgativo di un sistema in cui ci sono degli stati non conosciuti è il seguente: supponiamo che in un casinò al gioco dei dadi, casualmente si passi da un dado onesto a uno truccato con una certa probabilità e con un altro valore di probabilità si torni all’utilizzo del dado non truccato; in ogni momento non sappiamo quale sia il dado in uso; data l’osservazione dei risultati dal lancio dei dadi siamo in grado di stabilire se provengono dal dado truccato o dal dado regolare? Questo è uno dei problemi affrontabili con un Hidden Markov Model (HMM). In altre parole, posso osservare che c’è un sistema che evolve, ma non ho visibilità su quale sia il meccanismo che regola tale evoluzione; riesco a stabilire che il sistema evolve secondo un insieme di stati ma questi sono “nascosti”.
Gli Hidden Markov Models possono modellare in maniera “probabilistica” la dinamica di un sistema senza identificarne a priori le cause e gli stati sconosciuti sono identificabili solo attraverso le osservazioni, in maniera probabilistica.
Come gli HMM descrivono l’evoluzione di un sistema
Nella figura seguente è rappresentato schematicamente lo scenario minimo di un HMM.
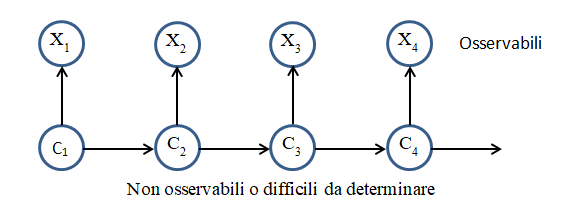
Un HMM modella un sistema come una serie di osservazioni {Xt }che evolve nel tempo e un insieme di stati nascosti {Ct }non noti a priori. Si possono stimare gli stati {Ct } più probabili che hanno generato le osservazioni {Xt } o anche, dato un insieme di stati interni {Ct } si possono calcolare le probabilità di ottenere le osservazioni {Xt }. Gli stati {Ct }, invisibili, costituiscono una catena di Markov e la distribuzione di probabilità delle osservazioni {Xt } dipende dagli stati sottostanti.
Ricordiamo che le catene di Markov sono basate sulla matrice di transizione e sulla probabilità di osservare una determinata sequenza di stati noti, ovvero che il sistema evolva secondo una determinata sequenza di stati; data la matrice di transizione è possibile determinare come evolverà il sistema e la probabilità che si trovi in uno specifico stato ad un determinato istante temporale.
Negli HMM sono previste due probabilità:
- la probabilità di transizione, relativa alla transizione fra gli stati (nascosti)
- la probabilità di emissione, ovvero di “emettere” una data osservazione quando il sistema si trova in una determinata combinazione di stati nascosti.
Un HMM può risolvere tre tipi di problemi:
- evaluation: si ricava la probabilità che il sistema si trovi in un determinato stato in uno specifico instante di tempo sulla base delle osservazioni emesse, ovvero si cerca lo stato che massimizza tale probabilità. Si risponde alla domanda: data una sequenza di eventi osservati qual è la probabilità che essa sia stata generata dal modello?
- decoding: si determina la sequenza degli stati interni (nascosti) del sistema data una sequenza di osservazioni degli stati esterni; questo compito viene svolto dall’algoritmo di Viterbi. Tra tutte le possibili combinazioni di stati si stabilisce la più probabile, la combinazione di stati che genera con probabilità massima la serie di osservazioni.
- training: si ricava la probabilità a posteriori di un’osservazione e la probabilità di transizione dato uno specifico stato interno; in altre parole, data una collezione di sequenze annotate, questa viene utilizzata per addestrare un modello. Questo compito viene svolto dall’algoritmo di Baum Welch.
Le tre procedure possono anche essere utilizzate insieme nella valutazione di un modello complesso, una non esclude le altre.
Hidden Markov Models: alcune applicazioni
Modellare un sistema in due livelli, uno visibile e uno invisibile, risulta vantaggioso in molti scenari reali. Di seguito sono riportati alcuni casi di applicazioni efficaci degli Hidden Markov Models che ci fanno capire come possano essere utilizzati insieme o in alternativa ad altri algoritmi di apprendimento usati nel Machine learning e nel Deep learning.
Per esempio, consideriamo l’Automatic Speech Recognition (ASR – trascrizione da vocale in testo) dove gli HMM sono stati usati in modo intensivo; il modello predice una sequenza di parole partendo dall’analisi di un segnale audio. In questo caso il sistema di riconoscimento cerca di trovare la sequenza di fonemi (gli stati nascosti) che generano il suono corrispondente (osservazione ovvero ascolto della lingua parlata); la grande variabilità e diversità nella pronuncia e le inflessioni fanno in modo che i fonemi originali non possano essere “osservati” quindi devono essere predetti massimizzando la probabilità.
Applicazioni in bioinformatica, studio sequenze DNA
Questi modelli hanno avuto molto successo con l’applicazione alla bioinformatica per l’analisi delle sequenze di DNA e per il riconoscimento di sequenze simili; nel caso specifico del DNA la sfida è capire analizzando una sequenza quali sono le coppie di basi prevalenti in tale sequenza. Nel caso dell’analisi delle proteine, si sa che due proteine con la stessa funzione possono essere differenti nella sequenza di aminoacidi perché ci sono state delle inserzioni o delle cancellazioni o delle sostituzioni di aminoacidi simili; il problema è stabilire se due sequenze simili possono essere la stessa proteina. Tra gli stati nascosti si definiscono gli stati di inserzione, cancellazione, sostituzione di un aminoacido e le probabilità di transizione verso questi stati, permettono di stabilire quanto sono simili due proteine. Il successo nella bioinformatica è dato dalla possibilità di gestire sequenze di lunghezza variabile, dalla possibilità di eseguire lavori di allineamento, analisi strutturale e rilevazione di pattern, dal fatto che il modello statistico è molto robusto ed efficiente.
Intrusion Detection System – IDS
Un Intrusion Detection System (IDS) classico si basa su una knowledge base nota per riconoscere i tentativi di intrusione in un sistema informatico dall’analisi del traffico di rete e sugli host nella rete. Il punto debole di questa architettura è che non rileva intrusioni non classificate nella knowledge base. Per ovviare a questa limitazione sono stati già sviluppati sistemi basati su algoritmi di intelligenza artificiale che identificano eventi anomali rispetto al traffico normale e sono in grado di rilevare anche eventi mai visti precedentemente. L’utilizzo degli HMM in questo campo permette precisione e accuratezza molto elevate, dell’ordine del 98% e più. Gli stati nascosti sono rappresentati da traffico regolare e dalle diverse tipologie di traffico non regolare ovvero di attacco; inoltre, si possono contemplare anche attacchi di tipo multi-stage. Giusto per ribadirne l’utilizzo nell’ambito dei metodi statistici di apprendimento, spesso gli HMM sono l’ultimo passo di una pipeline di algoritmi di Machine learning tra cui riduzione della dimensionalità e clustering.
Controlli remoti dei pazienti
L’utilizzo degli HMM nella rilevazione delle anomalie è applicabile ad altri campi oltre che alla identificazione di intrusioni; per esempio, si possono rilevare le anomalie nel comportamento di persone e in particolare di pazienti che devono seguire delle cure e sono controllati in modalità remota. Ci sono pubblicazioni [4] di lavori sullo studio del “Remote Patient Monitoring” in cui l’utilizzo degli HMM è la parte principale del controllo del comportamento di un paziente. Siamo nel campo dell’Internet of Medical Things (IoMT) e degli smart device per uso domestico.

Named Entity Recognition
La Named Entity Recognition (NER) è la parte del Natural Language Processing che si occupa di classificare le parole in categorie predefinite come ad esempio luoghi, nomi di persona, organizzazioni, eventi, etc. Questo scenario in genere viene affrontato con algoritmi di Machine Learning, ma in alcuni casi è risultato efficace utilizzare anche un HMM [2]. Si tratta dell’applicazione alla lingua indiana che ha caratteristiche molto differenti dalle lingue europee; per esempio non ci sono le maiuscole, ci sono molti termini ambigui, non c’è uno standard, inoltre in India ci sono molte lingue e per ognuna di queste ci sono molte varianti, al punto da dover utilizzare la lingua inglese come lingua comune. Tutto questo accentua maggiormente il fatto che un classico sistema di NER per una lingua non ha la stessa efficacia se applicato a un’altra lingua. Nel caso specifico è risultato che un NER basato su HMM risulta indipendente da un particolare linguaggio e non richiede un esperto della lingua, un risultato notevole considerate le molte variabili in gioco.
Conclusioni
Gli Hidden Markov Models offrono, nell’ambito dei metodi statistici di apprendimento e di previsione, un approccio alternativo ad algoritmi noti e collaudati. La loro complessità e il formalismo portano a preferire algoritmi di Machine learning e Deep learning, tuttavia la ricerca in merito è molto attiva e non mancano scenari in cui un Hidden Markov Model dà le prestazioni migliori fra tutti i modelli disponibili. Non mancano utilizzi ibridi di modelli di Markov insieme a metodi di apprendimento sia supervisionati sia non supervisionati.
Riferimenti
[1] Langrock, MacDonald, Zucchini – Hidden Markov models for time series. Ed. CRC Press
[2] Named Entity Recognition using Hidden Markov Model – International Journal on Natural Language Computing (IJNLC) Vol. 1, No.4
[3] Multi-Layer Hidden Markov Model Based Intrusion Detection System https://www.mdpi.com/2504-4990/1/1/17
[4] Detecting Anomalous User Behavior in Remote Patient Monitoring https://arxiv.org/pdf/2106.11844.pdf





